Mit VPython können Körper wie z.B. Kugeln (sphere), Zylinder (cylinder), Kegel (cone), Quader (box), Pyramiden (pyramid) usw. im 3D-Raum dargestellt und animiert werden. Unter Animationen wird hier die schnelle Abfolge von statischen Bildern verstanden: Die Körper bewegen sich realitätsnah im 3D-Raum auf dem Bildschirm. Solche Darstellungen werden als Szene bezeichnet. Pendel- und Wurfbewegungen lassen sich so anschaulich darstellen.
Wenn Sie in die Python-Shell folgenden Quelltext eingeben
>>> from vpython import *
>>> sphere()
erscheint nach der Betätigung der Return-Taste, in ihrem Browserfenster eine Kugel.

VPython stellt auch Steuerelemente wie z.B. Buttons, Checkboxes, Menus, Radiobuttons, Sliders usw. zur Verfügung.
Um die Funktionsweise von VPython richtig zu verstehen ist es besonders wichtig, die Anordnung der Koordinatenachsen zu analysieren. Das Bild zeigt den Screenshot des Programms vp_box_arrow.py.

Den Quelltext dieses Programms sollten Sie ausführlich analysieren und testen.
In allen VPython-Programmen ist der Vektor vector(x,y,z) oder kurz vec(x,y,z) das wichtigste Gestaltungselement. Er bestimmt die Position, die Abmessungen und die Ausrichtung eines Körpers.
Ein Quader wird mit der Methode
box(pos=vec(0,0,0),size=vec(a,b,c),axis=vec(x,y,z), ...)
erzeugt.
Der Parameter pos(x,y,z) bestimmt die Position des Quaders. Sie liegt in seinem Schwerpunkt.
Für die Länge, Breite und Höhe des Quaders stehen die Argumente (a,b,c).
Der Parameter axis(x,y,z) bestimmt die Ausrichtung des Quaders.
Ein Pfeil wird mit der Methode
arrow(pos=vec(0,0,0), axis=vec(x,y,z), ...)
erzeugt. Der Parameter pos(x,y,z) bestimmt die Position des Pfeilanfangs (Pfeilfuß).
Der Parameter axis(x,y,z) legt die Ausrichtung des Pfeils fest.
Der Standardwert für die Position des Quader- und des Pfeil-Objektes ist das Attribut pos=vec(0,0,0)).
Der Standardwert für die Ausrichtung des Quader- und des Pfeil-Objektes ist das Attribut axis=vec(1,0,0)).
#!/usr/bin/env python3
#vp_box_arrow.py
from vpython import *
#Daten
L = 10 #Breite der Objekte
factor = 1.
a = factor*L #Laenge
b = factor*L #Breite
c = factor*L #Hoehe
sw=0.15
colK=color.black
#Grafikbereich
scene.title="Quader"
scene.width =800
scene.height=800
scene.background = color.white
scene.range=1.5*L #Zeichenbereich vergroeßern
scene.center=vector(0,0,0) #Position des Beobachters
scene.userzoom = False #kein Zoom
scene.userspin = True
#Der Ursprung des Koordinatensystems liegt
#in der Mitte der Zeichenfläche.
X=arrow(shaftwidth=sw,round=True,color=colK)
Y=arrow(shaftwidth=sw,round=True,color=colK)
Z=arrow(shaftwidth=sw,round=True,color=colK)
X.axis=vec(L, 0, 0)
Y.axis=vec(0, L, 0)
Z.axis=vec(0, 0, L)
#Beschriftung der Achsen
label(pos=1.05*L*vec(1,0,0),text='x')
label(pos=1.05*L*vec(0,1,0),text='y')
label(pos=1.05*L*vec(0,0,1),text='z')
#Quader: Breite, Hoehe, Tiefe
quader=box(size=vec(a,b,c),opacity=0.25,color=color.green)
quader.pos=vec(0,0,0) #Schwerpunkt
scene.caption='''\nDrücken Sie die rechte Maustaste und bewegen
Sie den Mauszeiger über die Zeichenfläche!'''
Die Standardwerte für die Positionsvektoren der Pfeile und des Quaders sind pos=vec(0,0,0).
Dieser Parameter fehlt im Programm. Sie können diesen Parameter für die Pfeile und den Quader entsprechend ergänzen
und das Programm mit geänderten Koordinatendaten testen.
Ein Slider-Objekt wird mit
sldObjektname = slider(bind=myaction, min=0, max=50, ... )
erzeugt. mayaction ist eine selbstdefinierte Python-Funktion, die den Ablauf der Ereignisverarbeitung festlegt.
Die zwei folgenden Programmbeispiele zeigen Möglichkeiten, wie das Slider-Steuerelement verwendet werden kann.
Das Bild zeigt den Screenshot des Programms vp_slider_zylinder. Das Programm berechnet das Trägheitsmoment eines Zylinders.
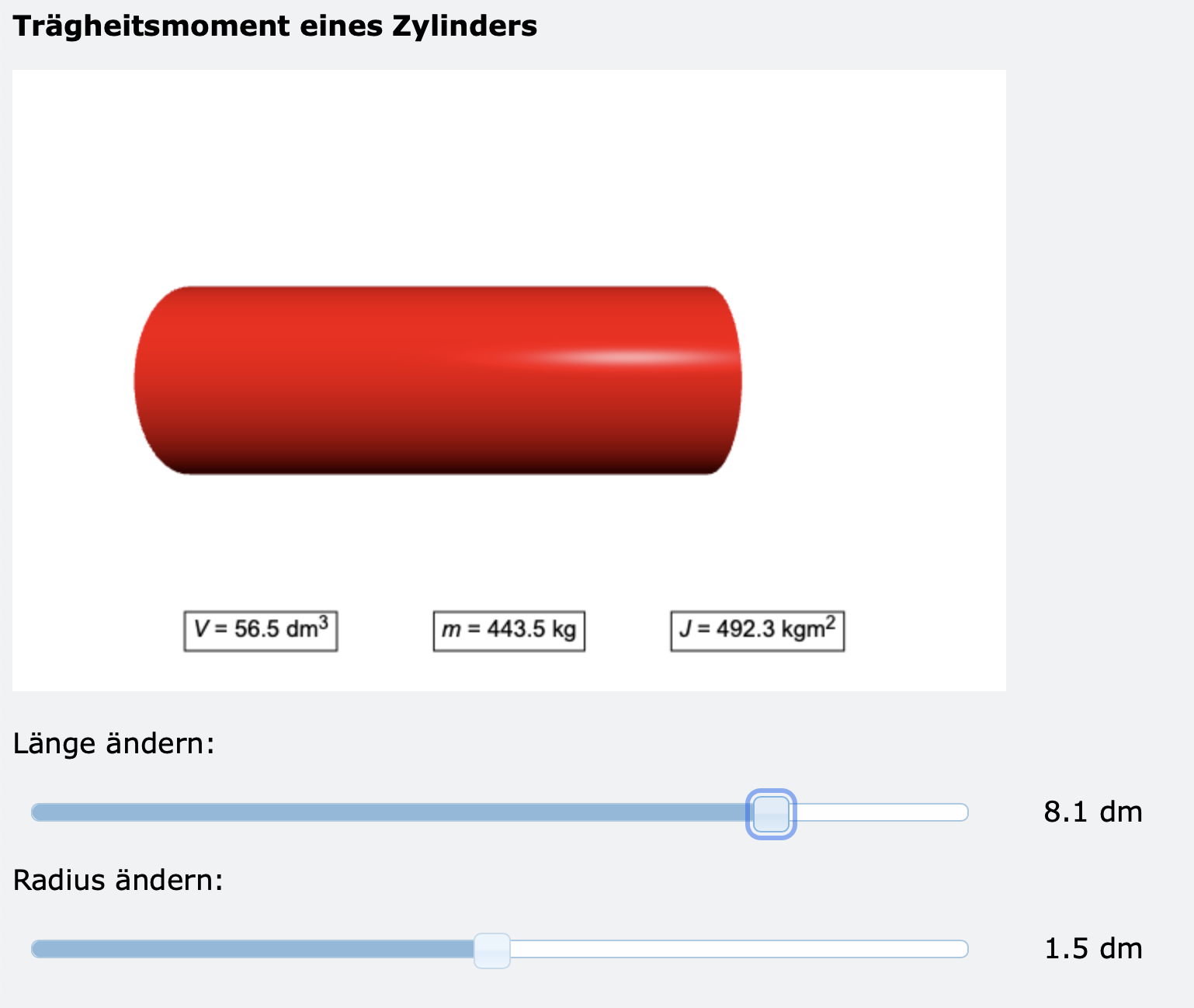
Wenn Sie einen der beiden Slider-Knöpfe verschieben, erscheint in der Ausgabe der Benutzeroberfläche der aktuelle Wert des Trägheitsmoments.
#!/usr/bin/env python3
#vp_slider_zylinder.py
from vpython import *
#Daten
l0=3
r0=1
rho=7.85 #Dichte von Stahl in kg/dm^3
#Berechnungen durchführen
def calc():
l=sldL.value #Länge
r=sldR.value #Radius
zylinder.length = l
zylinder.radius = r
V=pi*r**2*l #Volumen
m=rho*V #Masse
J=m*r**2/2*1e-2 #Trägheitsmoment
txtL.text=text='\t %2.1f dm' %l
txtR.text=text='\t %2.1f dm' %r
lblV.text = 'V = %2.1f dm3' %V
lblM.text = 'm = %2.1f kg' %m
lblJ.text = 'J = %2.1f kgm2' %J
#Grafikbereich
scene.title="Trägheitsmoment eines Zylinders"
scene.background = color.white
scene.range=5
#Zyliderobjekt erzeugen
zylinder = cylinder(pos=vec(-5,0,0),color=color.red)
zylinder.axis=vec(l0,0,0)
zylinder.radius=r0
#Slider: Länge ändern
scene.caption = "\nLänge ändern: \n\n"
sldL = slider(bind=calc,min=1,max=10,value=l0,length=650)
txtL = wtext(text='\t %2.1f dm' %sldL.value)
#Slider: Radius ändern
scene.append_to_caption("\n\nRadius ändern: \n\n")
sldR = slider(bind=calc,min=1,max=2,value=r0,length=650)
txtR = wtext(text='\t %2.0f dm' %sldR.value)
scene.append_to_caption("\n\n")
#Ergebnisse ausgeben
lblV = label(pos=vec(-4,-4,0),text='V = %2.1f dm3' %0)
lblM = label(pos=vec(0,-4,0),text='m = %2.1f kg' %0)
lblJ = label(pos=vec(4,-4,0),text='J = %2.1f kgm2' %0)
Die HTML-Formatierungen des VPython-Quelltextes werden im Browser nicht angezeigt. Wenn Sie den Quelltext mit den formatierten Ausgaben kopieren möchten, dann müssen Sie auf DOWNLOAD klicken. Der VPython-Quelltext wird dann in einem neuen Tab als Text ohne Formatierung in Ihrem Browserfenster angezeigt. Mit [Strg] + [A] markieren Sie den Quelltext und mit [Strg] + [C] können Sie ihn in die Zwischenablage kopieren und anschließend mit [Strg] + [V] in Ihre Python-Entwicklungsumgebung einfügen.
Das Bild zeigt den Screenshot des Programms vp_actio_reactio.py. Mit diesem Programm kann das dritte Newtonsche Axiom veranschaulicht werden.

Wenn Sie den Slider-Knopf verschieben, werden die beiden Federkräfte neu berechnet und in der Benutzeroberfläche angezeigt.
#!/usr/bin/env python3
#vp_actio_reactio.py
from vpython import *
kf=10 #Federkonstante N/cm
x0=5 #Startwert für Dehnung
#Funktionsdefinion für Dehnung
def weg(s):
pfeilFa.pos=feder.pos + vector(s.value,0,0)
pfeilFa.axis.x = s.value #nach rechts
pfeilFr.axis.x = -s.value #nach links
feder.axis.x = s.value
F=kf*s.value #Federkraft
lblFa.text = 'Fa = %2.1f N' %F #actio
lblFr.text = 'Fr = -%2.1f N' %F #reactio
txtWeg.text = '\t %2.2f' %s.value
#Graphikbereich
...
Animationen werden innerhalb einer while-Schleife ausgeführt:
while True:
rate(n)
...
Die rate(n)-Anweisung hält Berechnungen bei Bedarf lange genug an, um sicherzustellen, dass mindestens 1/n Sekunde vergangen ist.
In einem VPython-Programm ist die Funktion rate() ist ein wesentlicher Bestandteil der Animationsschleife. rate(n) erfüllt vier wichtige Aufgaben:
Ein typisches Beispiel ist die Animation eines Balls, der sich zwischen zwei Wänden hin und her bewegt. Das Bild zeigt den Screenshot einer Momentaufnahme des VPython-Programms vp_ball_wand.py.

Testen Sie das Programm auch mit anderen Radien und Wanddicken. Wenn Sie das Programm gestartet haben, können Sie durch Drehen der Szene die Ballbegung aus verschiedenen Perspektiven betrachten.
#!/usr/bin/env python3
#vp_ball_wand.py
from vpython import *
#Daten
R=0.5 #Radius des Balls
dicke=0.25 #Dicke der Waende
x1=x2=5 #Abstand vom Koordinatenursprung
#Grafikbereich
scene.background=color.white
scene.width=scene.height=600
scene.range=1.5*x1
scene.userzoom=False
#Waende erzeugen
box(pos=vec(-x1,0,0),size=vec(dicke,5,5),opacity=0.5)
box(pos=vec( x2,0,0),size=vec(dicke,5,5),opacity=0.5)
#Ballobjekt erzeugen
ball=sphere(radius=R,color=color.red)
d = x1 - dicke/2 - R #1
dx=0.1 #2
while True: #3
rate(30) #4
x = ball.pos #5
x = x + vec(dx,0,0) #6
ball.pos = x #7
if (x.x <= -d or x.x >= d): #8
dx=-dx #9
Zu beachten ist, dass sich der Koordinatenursprung in der Mitte der Zeichenfläche befindet.
#1: Hier wird der halbe Abstand zwischen den Wänden berechnet.
#2: dx ist das Weginkrement. Bei jedem neuen Schleifendurchlauf wird die Position des Balls um diesen Betrag nach links oder rechts verschoben.
#3: Es wird eine Endlosschleife implementiert.
#4: Die Position des Balls wird 30 mal in der Sekunde verändert.
#5: Der Variablen x wird die Position des Balls zugewiesen. Da ball.pos ein Vektor ist, ist x auch eine Vektor.
#6: Die x-Komponente des Vektors x wird um den Betrag dx verschoben.
#7: Dem Vektor ball.pos wird der aktuelle Wert des Vektors x zugewiesen.
#8: Wenn die Position von x.x kleiner gleich -d oder größer gleich d wird eine Richtungsänderung erzwungen.
#9: Die Vorzeichenumkehr erzwingt die Richtungsänderung.
Das Beispiel zeigt, wie mit VPython die Pendelbewegung eines Fadenpendels im 3D-Raum animiert werden kann.
Die Pendelbewegung eines Fadenpendels wird durch zwei Differenzialgleichungen erster Ordnung beschrieben:
\[\frac{d\varphi }{dt} =\omega \]
\[\frac{d\omega }{dt} =-\frac{g}{l} \sin \varphi \]
Dieses DGL-System lässt sich leicht mit einfach zu implementierende und ressourcenschonende Euler-Verfahren numerisch lösen.
Der Quotient aus der Gravitationskonstanten g und der Pendellänge l bestimmt die Anzahl der Schwingungen pro Sekunde (Frequenz f). Für die Frequenz gilt:
\[f=\frac{1}{2\pi} \sqrt{\frac{g}{l}}\]
Das Bild zeigt den Screenshot einer Momentaufnahme des Programms vp_fadenpendel.py.
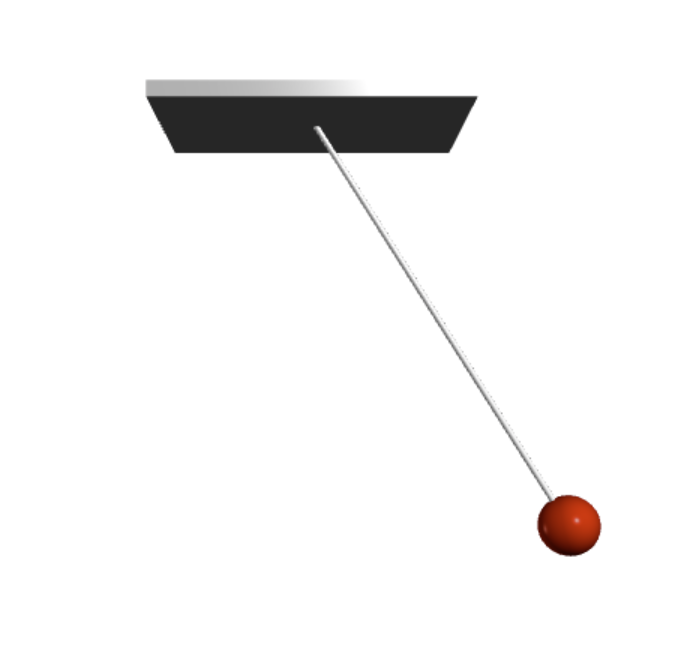
In Zeile 5 können Sie die Pendellänge ändern. Sie beeinflusst die Schwingungsdauer.
#!/usr/bin/env python3
#vp_fadenpendel.py
from vpython import *
#Daten
l=8 #Länge des Pendels
phi=45 #Auslenkung
b=5 #Breite der Decke
R=0.5 #Radius der Kugel
g=9.81 #Erdbeschleunigung
w02=g/l #Quadrat der Kreisfrequenz
phi=radians(phi)
w=0. #Anfangswinkelgeschwindigkeit
dt=1e-2 #Zeitschrittweite
#Grafikbereich
scene.width=600
scene.height=600
scene.center=vector(0,l/3,0)
scene.range=1.5*b
scene.background = color.white
scene.userzoom = False #kein Zoom
decke=box(size=vec(b,b/20.,b/2.),color=color.gray(0.8))
decke.pos=vec(0,l,0)
stange=cylinder(axis=vec(0,l,0),radius=0.05)
stange.pos=vec(0,l,0)
masse = sphere(radius=R,color=color.red)
masse.pos=vec(0,stange.pos.y,0)
#Animationsschleife
while True: #Endloßschleife
rate(100) #Wiederholungen pro Sekunde
phi=phi + w*dt #Lösung der DGL
w=w - w02*sin(phi)*dt #mit dem Eulerverfahren
x= l*sin(phi) #x-Koordinaten berechnen
y=-l*cos(phi) #y-Koordinaten berechnen
stange.axis=vec(x,y,0)
masse.pos=stange.pos + vec(x,y,0)
Nach dem Start des Programms schwingt das Pendel im virtuellen 3D-Raum des Browserfensters. Bei jedem Durchlauf der while-Schleife bewegt sich das Pendel um den Betrag des Winkels ω⋅dt. Durch die Änderung der Zeitschrittweite dt kann man die Geschwindigkeit der Pendelbewegung beeinflussen. Das DGL-System wird mit dem Summenalgorithmus des Euler-Verfahrens gelöst. Die Dämpfung wurde nicht berücksichtigt.
Der Bewegungsverlauf eines Feder-Masse-Schwingers lässt sich durch das folgende Differenzialgleichungssytem beschreiben:
\[\frac{dx}{dt} = v\]
\[\frac{dv}{dt} =-\frac{k_{f}}{m} x-\frac{b}{m} v \]
Die Konstante b bestimmt die Dämpfung. Sie ist proportional zur Geschwindigkeit.
kf ist die Federkonstante. Der Quotient aus Federkonstante und Masse m legt die Anzahl
der Schwingungen pro Sekunde fest. Für die Frequenz gilt:
\[f=\frac{1}{2\pi} \sqrt{\frac{k_{f}}{m}}\]
Das Bild zeigt den Screenshot des Programms vp_federpendel.py.
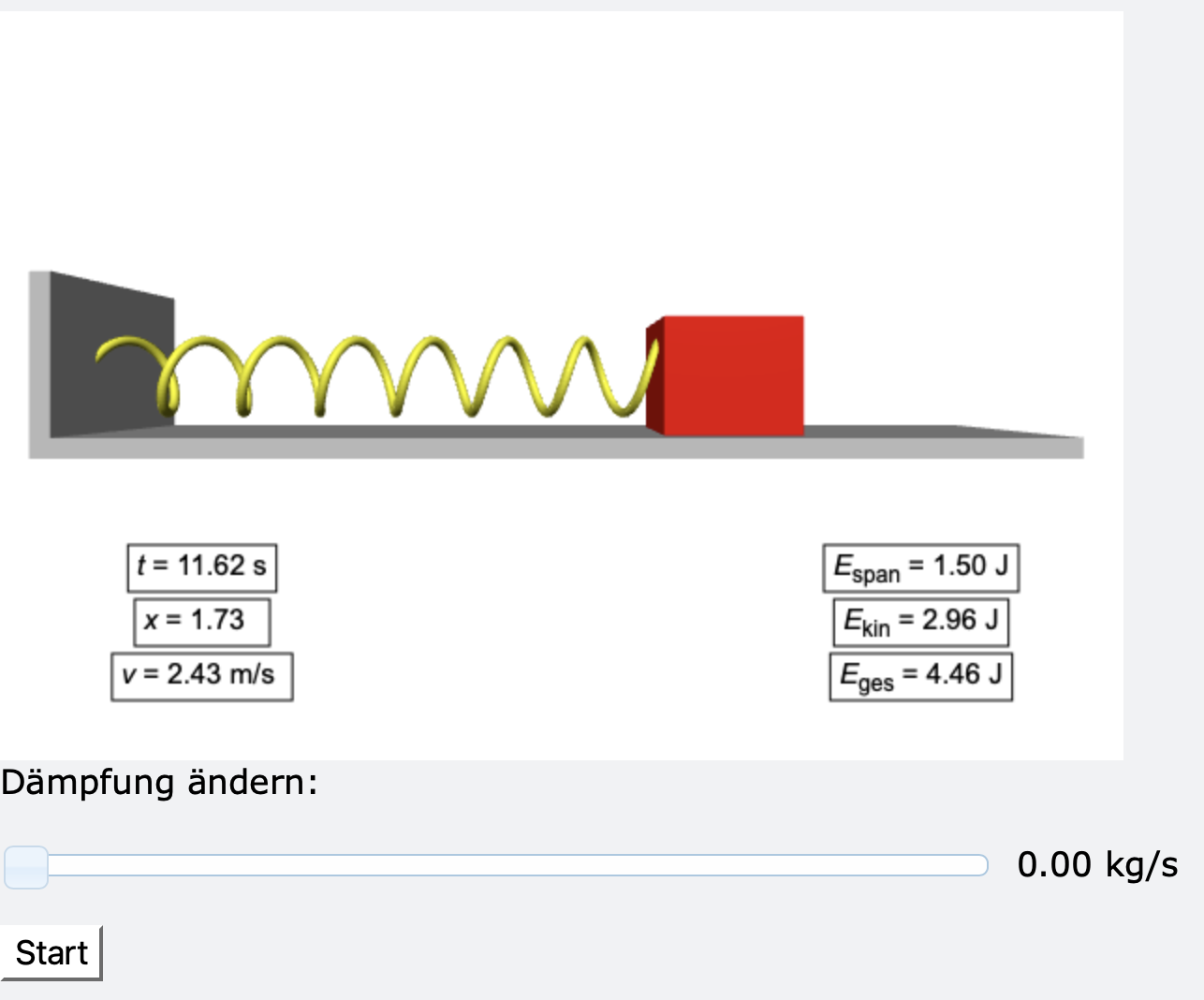
Mit den Slider können Sie die Dämpfung einstellen. Wenn man sich vorstellt, dass sich die Masse auf einem Luftkissen bewegt, dann verläuft die Bewegung nahezu ohne Reibung.
#!/usr/bin/env python3
#vp_federpendel.py
from vpython import *
#Daten
kf=1.0 #Federkonstante N/m
m=1.0 #Masse des Wuerfels in kg
w02 = kf/m #Quadrat der Kreisfrequenz
x = 3 #Anfangswert der Auslenkung
v = 0 #Anfangsgeschwindigkeit
...
#Animationsschleife
while True:
rate(100)
b=sldB.value #Wert fuer Daempfungskonstante kg/s
if run:
#Loesung der DGL mit dem Euler-Verfahren
x = x + v*dt #Weg
v = v - w02*x*dt - b/m*v*dt #Geschwindigkeit
#Energien berechnen
Espan=0.5*kf*x**2 #Spannenergie
Ekin=0.5*m*v**2 #kinetische Energie
Eges = Ekin + Espan
#Feder-Masse-System darstellen
feder.axis= vector(x + x0,0,0) #Feder
masse.pos = vector(x,0,0) #Masse
t+=dt
#Ausgabe der aktuellen Energien
lblT.text= 't = %2.2f s' %t
lblX.text= 'x = %1.2f ' %x
lblV.text= 'v = %1.2f m/s ' %v
lblEspan.text= 'Espan = %1.2f J' %Espan
lblEkin.text = 'Ekin = %1.2f J' %Ekin
lblEges.text = 'Eges = %1.2f J' %Eges
else:
v=0 #neuer Anfangswert fuer Geschwindigkeit
x=3 #neue Auslenkung
t=0 #Zeit zuruecksetzen
Den vollständigen Quelltext anzeigen.
Nach dem Programmstart werden Sie feststellen, dass die Summe aus Spannenergie und kinetischer Energie nicht zu jedem Zeitpunkt konstant ist. Dieser Widerspruch zur Theorie lässt sich durch Rundungsfehler erklären.
In vielen Sportdisziplinen (Golf, Tennis, Fußball, Handball, Kugelstoßen, Hammerwurf, usw.) kommt der schiefe (oder schräge) Wurf vor. Den Physiker interessiert unter anderem die Form der Wurfbahn, die Wurfzeit, die Wurfweite und die Wurfhöhe. Wenn ein Ball geworfen wird, muss er den Luftwiderstand überwinden. Das legt die Vermutung nahe, dass sich unter dem Einfluss des Luftwiderstandes die Wurfweite - im Vergleich zu idealisierten Annahmen- verringern wird. Die Wurfbahn soll zunächst ohne Luftwiderstand animiert werden. Die Anfangsgeschwindigkeit v0 und der Abwurfwinkel α sind die wichtigsten Einflussgrößen auf die Wurfweite.
Das Bild zeigt eine Wurfbahn. Zu verschiedenen Zeitpunkten sind die Geschwindigkeitskomponenten eingezeichnet.
Im Maximum der Kurve verschwindet die y-Komponente des Geschwindigkeitsvektors.
Der Geschwindigkeitsvektor kann in seine x- und y-Komponente zerlegt werden. Für x-Komponente des Geschwindigkeitsvektors gilt dann:
\[ v_{x}=v_{0}\cos \left( \alpha \right) \qquad (1)\]
Während der gesamten Wurfdauer ist die Geschwindigkeitskomponente in x-Richtung konstant.
Für y-Komponente des Geschwindigkeitsvektors gilt entsprechend:
\[v_{y}=v_{0}\sin \left( \alpha \right) - g\cdot t \qquad (2)\]
Gl. (2) hat eine bei t1 = v0·sinα/g ein Maximum. Bis zu dem Zeitpunkt t < t1 zeigt y-Komponente des Geschwindigkeitsvektors in Richtung der positiven y-Achse. An der Stelle t = t1 ist die y-Komponente des Geschwindigkeitsvektors gleich null. Für t > t1 zeigt y-Komponente des Geschwindigkeitsvektors in Richtung der negativen y-Achse.
Durch Integration von Gl. (1) und Gl. (2) erhält man die Wegkomponenten. Für die x-Komponente des Weges gilt dann:
\[\ x=v_{0}\cos \left( \alpha \right) \cdot t \qquad (3)\]
und für die y-Komponente des Weges gilt:
\[\ y\ =v_{0}\sin \left( \alpha \right) \cdot t\ -\ \frac{1}{2} g\cdot t^{2} \qquad (4)\]
Wenn man Gl. (3) nach t auflöst und in Gl. (4) einsetzt, erhält man die Gleichung einer nach unten geöffneten Parabel:
\[ y=\tan \left( \alpha \right) \cdot x-\ \frac{g}{2v_{0}^{2}\cos^{2} \left( \alpha \right)} x^{2} \qquad (5)\]
Ein geworfener Ball bewegt sich also auf einer parabelförmigen Wurfbahn.
Die Wurfzeit tw erhält man, indem man Gl. (4) gleich null setzt und die Gleichung nach t auflöst:
\[t_{w}=\frac{2v_{0}\sin \left( \alpha \right)}{g} \qquad (6)\]
Die Wurfweite xw erhält man, indem man Gl. (6) in Gl. (3) einsetzt:
\[\ x_{w}=\frac{v_{0}^{2}\sin \left( 2\alpha \right)}{g} \qquad (7)\]
Die Wurfhöhe ymax erhält man, indem man die halbe Wurfzeit von Gl. (6) in Gl. (4) einsetzt:
\[\ y_{max}=h=\frac{v_{0}^{2}\sin^{2} \left( \alpha \right)}{2g} \qquad (8)\]
Das Bild zeigt den Screenshot des VPytnon-Programms vp_wurf.py.
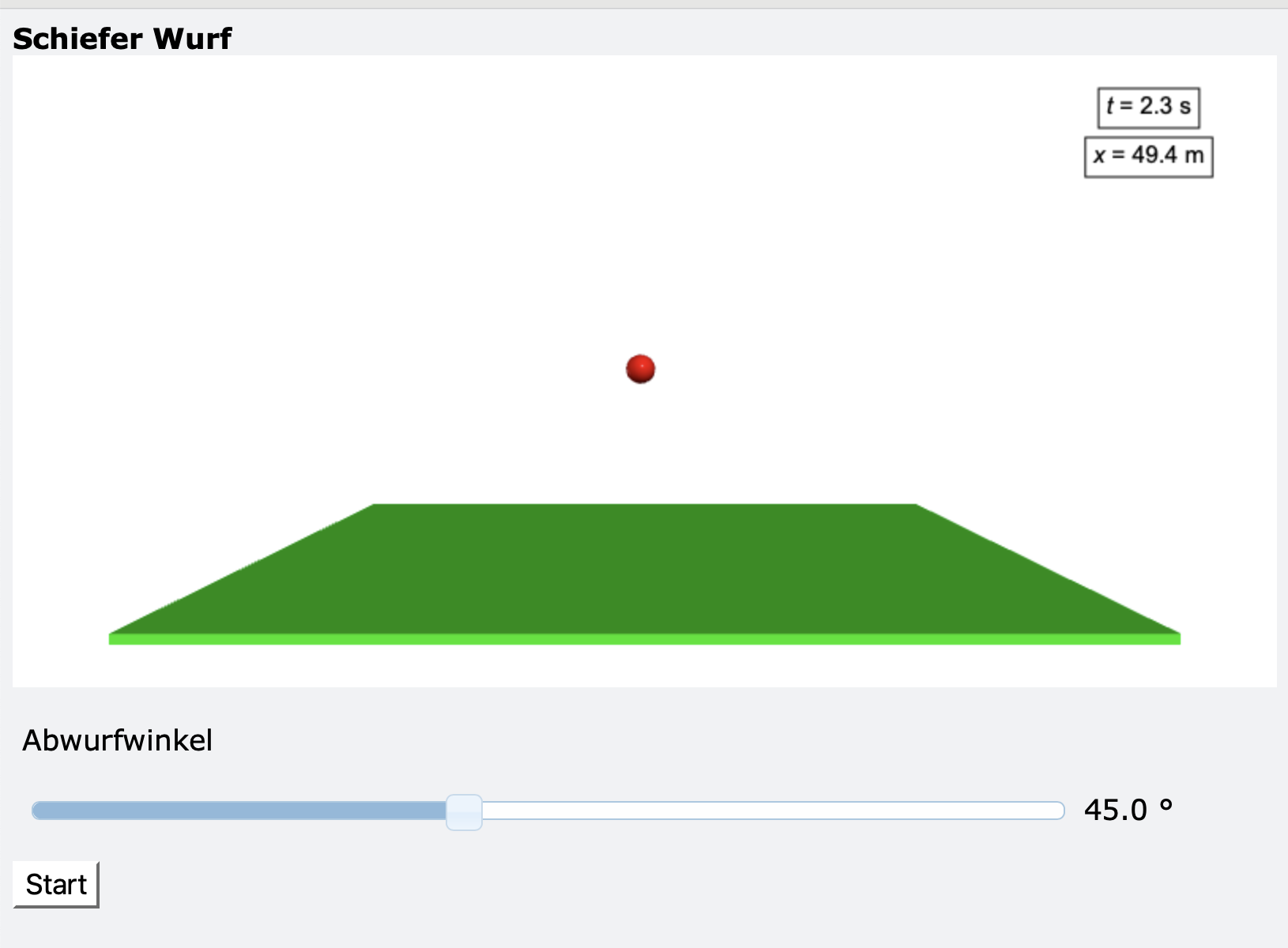
Durch Verschieben des Slider-Knopfes können Sie den Einfluss des Abwurfwinkels auf die Wurfzeit und Wurfweite untersuchen.
#!/usr/bin/env python3
#vp_wurf.py
from vpython import *
#Daten
v0=30 #Anfangsgeschwindigkeit
R = 2 #Z6: Radius des Balls
laenge=100 #Z7: Länge der Bodenplatte
dicke = 1 #Hoehe der Bodenplatte
g=9.81 #Erdbeschleunigung
dt=1e-2 #Zeitschrittweite
...
#Animationsschleife
t=x=y=tw=0
while True:
rate(30)
if not run:
alpha=radians(sldWinkel.value)
if run:
x = v0*cos(alpha)*t
y = y0 + v0*sin(alpha)*t - g*t**2/2
ball.pos=vec(x - laenge/2,y,0)
tw=t
t+=dt
if y < y0: #Ball erreicht den Boden
t=y=0 #Z63
run = False
if run == False:
cmdS.text="Start"
#Ausgabe für Wurfzeit und Wurfweite
lblTw.text = 't = %2.1f s' %tw
lblXw.text = 'x = %2.1f m' %x
In Zeile 6 wird der Radius des Balls mit zwei Längeneinheiten (LE) festgelegt. Dieser Wert ist im Vergleich zur Länge von 100 LE (Zeile 7) nicht maßstabsgetreu. Ein Fußballfeld hat eine Länge von 105 m. Ein normaler Fußball hat einen Durchmesser von 22 cm. Ein Fußballfeld ist also um den Faktor 477 länger als der Durchmesser eines Fußballs. Das Verhältnis von Fußballdurchmesser zu Fußballfeld beträgt also etwa 2 ‰. Bewegen Sie die Szene mit der rechten Maustaste. Sie können so den Wurf aus verschiedenen Perspektiven beobachten. Ermitteln Sie den Abwurfwinkel für die maximal mögliche Wurfweite. Überprüfen Sie, ob die von Programm ermittelte Wurfweite realistisch ist.
Mit dem Programm vp_wurf.py können Sie die Momentangeschwindigkeiten näherungsweise bestimmen, indem Sie die Ausführung an verschiedenen Wurfpositionen anhalten, die zugehörigen Zeiten und Wegabschnitte aufschreiben und aus den Differenzen die Geschwindigkeiten vi = Δsi/Δti berechnen.
Den vollständigen Quelltext anzeigen.
Die Wurfweite ist abhängig vom Luftwiderstand, der Masse und der Form des zu bewegenden Körpers (z.B.Kugel). In der Tabelle sind alle relevanten Daten, die die Wurfweite beeinflussen, für Golf, Tennis, Kugelstoßen und Fußball aufgelistet.
| Durchmesser | Masse | Anfangsgeschwindigkeit | |
|---|---|---|---|
| Golfball | 43 mm | 45 g | 48 m/s |
| Tennisball | 6,54 bis 7,86 cm | 56,0 bis 59,4 g | 56 m/s |
| Kugelstoßen | 11 bis 13 cm | 7,26 kg | 14 m/s |
| Hammerwurf | 11 bis 13 cm | 7,26 kg | 28 m/s |
| Fußball | 22 cm | 410 bis 450 g | 42 m/s |
Der Luftwiderstand ist proportional zur Querschnittsfläche A und zum Quadrat der Geschwindigkeit v eines Körpers:
\[ F_{w}=\frac{1}{2} \varrho \cdot c_{w}\cdot A\cdot v^{2} = b\cdot v^{2}\qquad (9)\]
Die Luftdichte hat bei 15° Celsius einen Wert von ρ = 1,225 kg/m3. Die Konstante cw, der Strömungswiderstandskoeffizient, ist abhängig von der Form des Körpers. Für eine Kugel kann sie Werte zwischen 0,2 und 0,4 annehmen.
Der schiefe Wurf mit Luftwiderstand kann durch folgendes DGL-System beschrieben werden:
\[ \frac{dx}{dt} =v_{x} \]
\[ \frac{dv_{x}}{dt} =-\frac{1}{m} b\cdot v\cdot v_{x} \]
\[ \frac{dy}{dt} =v_{y} \]
\[ \frac{dv_{y}}{dt} =-g-\frac{1}{m} b\cdot v\cdot v_{y} \]
Für den Betrag der resultierenden Geschwindigkeit v gilt:
\[\ v=\sqrt{v_{x}^{2}\ +\ v_{y}^{2}}\]
Das DGL-System ist nicht linear, es kann also nur numerisch gelöst werden. Gewählt wird wieder das Euler-Verfahren. Das Bild zeigt den Screenshot des Programms vp_realer_wurf.py.
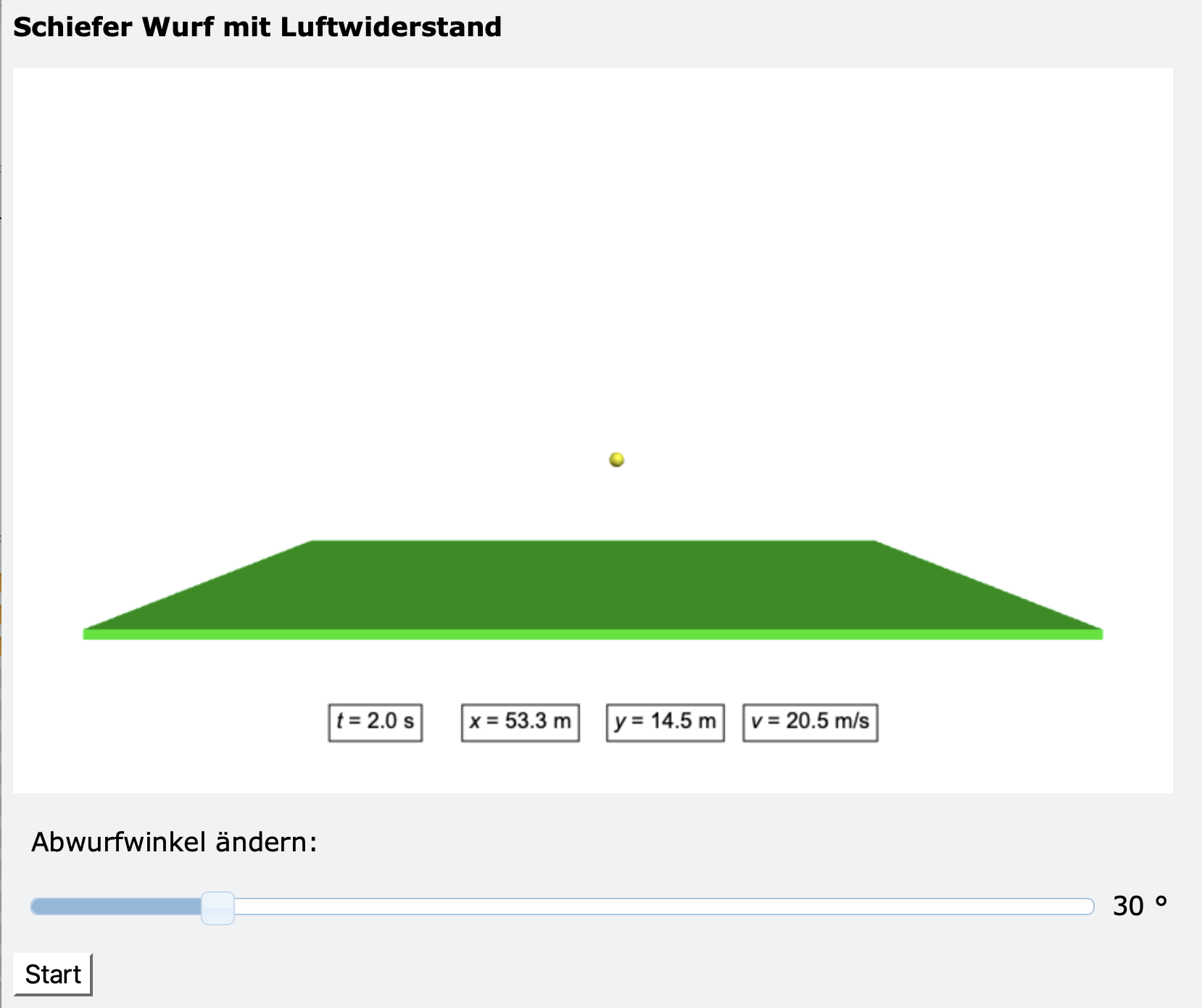
In den Zeilen 5 bis 8 können Sie andere Daten eingeben.
#!/usr/bin/env python3
#vp_realer_wurf.py
from vpython import *
#Daten
v0=42 #Anfangsgeschwindigkeit
m=0.45 #Masse der Kugel in kg
d=0.22 #Durchmesser der Kugel in Meter
cw=0.2 #Stroemungswiderstandskoeffizient
rho=1.225 #Luftdichte in kg/m^3
...
while True:
rate(30)
if not run:
t=x=vx=vy=0
y=y0
alpha=radians(sldWinkel.value)
vx=v0*cos(alpha)
vy=v0*sin(alpha)
if run:
v=sqrt(vx**2 + vy**2)
vx = vx - b*vx*v*dt/m
vy = vy - g*dt - b*vy*v*dt/m
x = x + vx*dt
y = y + vy*dt
ball.pos = vec(x - laenge/2,y,0)
h=y #Wurfhoehe
xw=x #Wurfweite
tw=t #Wurfzeit
t+=dt
if y < y0: #Ball erreicht den Boden
t=x=vx=vy=0
y=y0
run=False
if run == False:
cmdS.text="Start"
...
Den vollständigen Quelltext anzeigen.
Wenn Sie das Programm für verschiedenen Szenarien testen, werden Sie feststellen, dass beim Kugelstoßen und beim Hammerwurf der Einfluss des Luftwiderstandes am geringsten ist.
Mit VPython können auch 2D- und 3D-Funktionsplots dargestellt werden. Das erste Beispiel zeigt den Verlauf des Luftwiderstandes Fw = f(v) (Gl. 9). Verglichen wird der Luftwiderstand eines Fußballs mit dem Luftwiderstand eines Tennisballs.
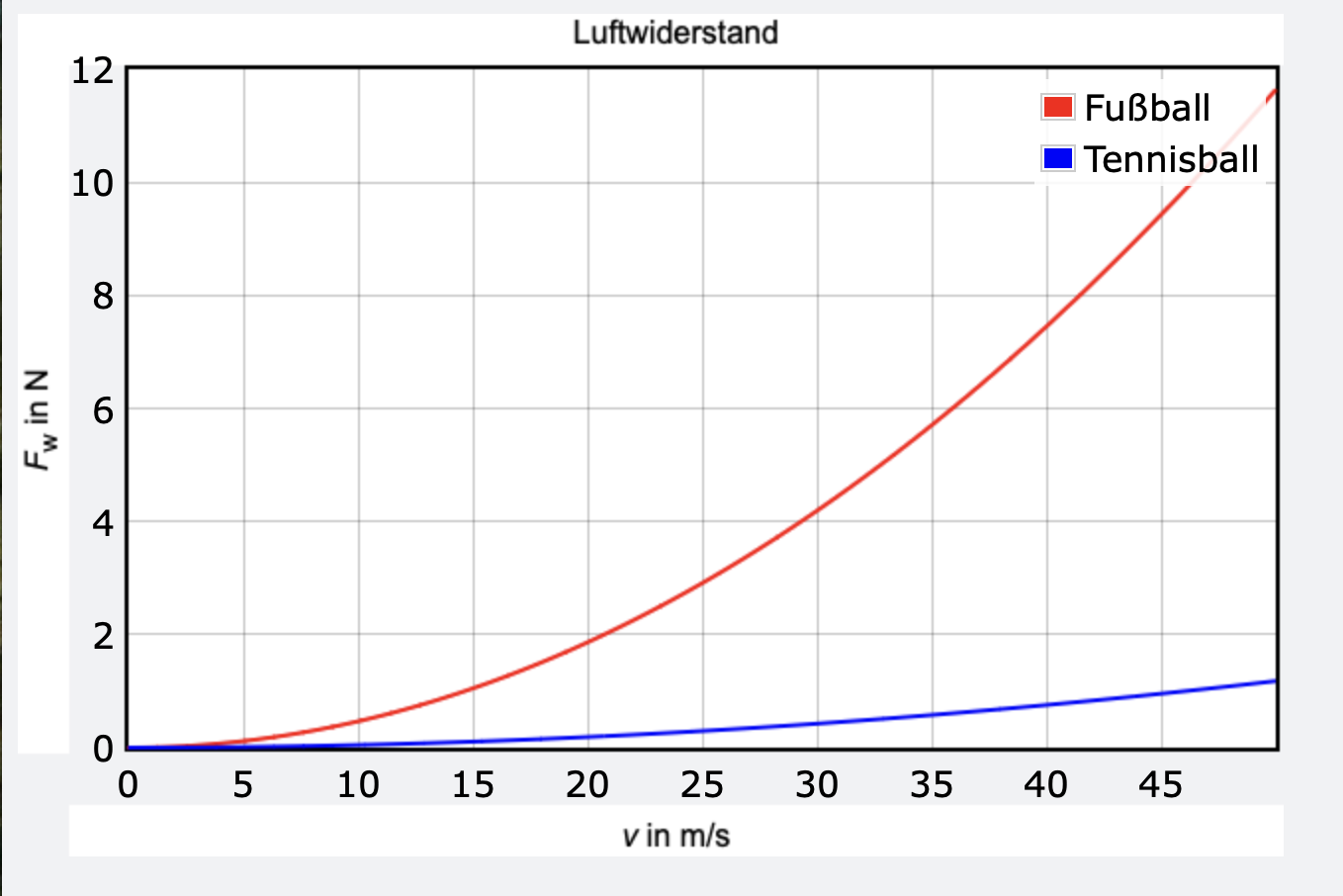
Funktionsplots werden mit der Methode plot() erstellt.
#!/usr/bin/env python3
#vp_plot_luftwiderstand.py
from vpython import *
#Daten
d1=0.22 #Fussball
d2=0.07 #Tennisball
cw=0.2
rho=1.225 #Luftdichte in kg/m^3
#Funktionsdefinition fuer Querschnitt
def querschnitt(d):
return pi*(d/2)**2
#Funktionsdefinition fuer Luftwiderstand
def luftwiderstand(v,d):
b=0.5*rho*cw*querschnitt(d)
return b*v**2
#fuer Beschriftungen
graph(title='Luftwiderstand',\
xtitle='v in m/s',\
ytitle='Fw in N')
#Objekte fuer Funktionsdarstellung erzeugen
y1 = gcurve(color=color.red,width=2,label='Fußball')
y2 = gcurve(color=color.blue,width=2,label='Tennisball')
#Kurve zeichnen
for v in arange(0,50,1e-2):
y1.plot(v,luftwiderstand(v,d1))
y2.plot(v,luftwiderstand(v,d2))
Die plot-Methode von VPython muss innerhalb einer Schleife ausgeführt werden.
Das zweite Beispiel zeigt die Funktionsplots für den idealen und realen schiefen Wurf.
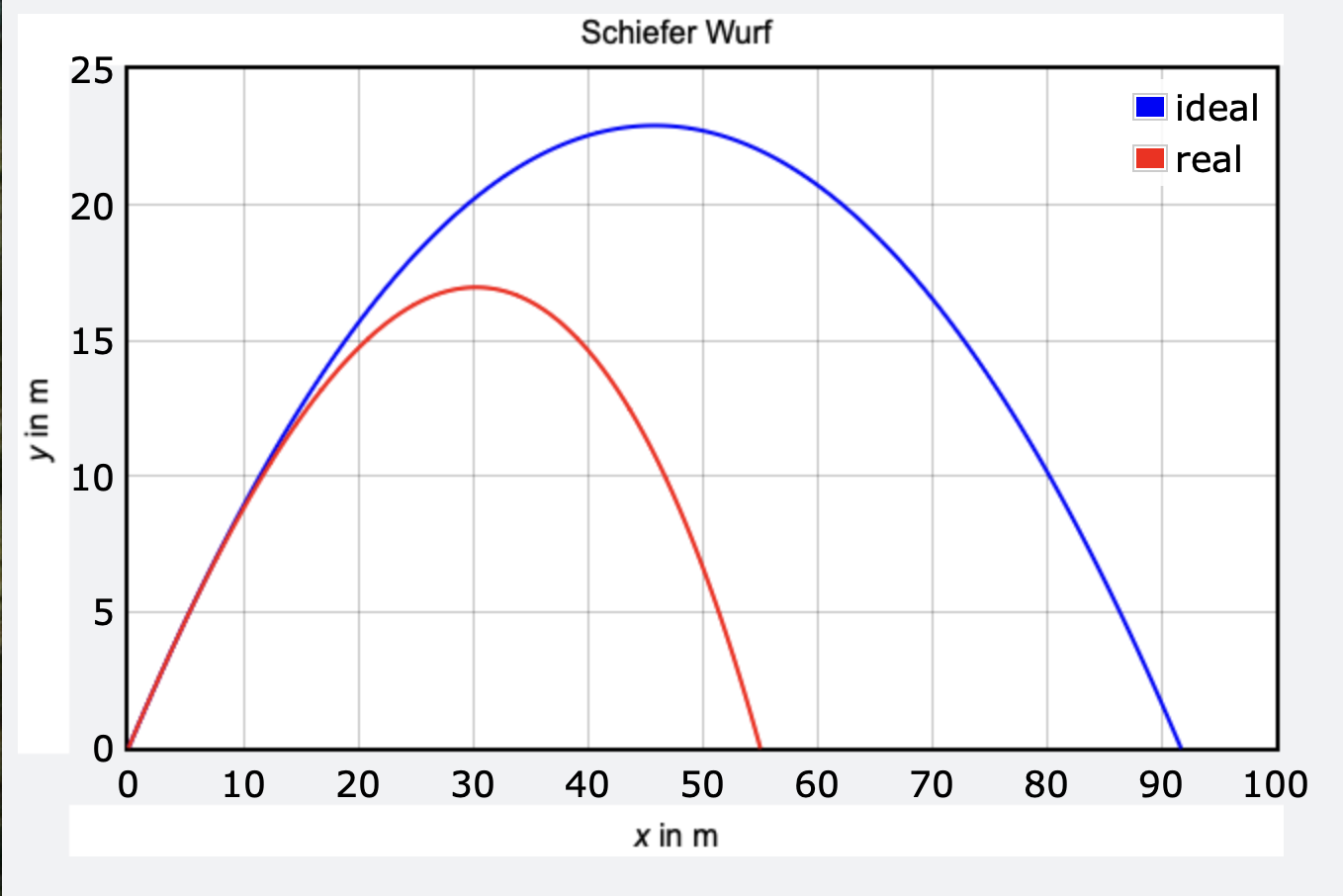
Das DGL-System wird mit dem Euler-Verfahren gelöst. Der ideale Verlauf des schiefen Wurfs wird erzwungen, indem der Dämpfungskonstanten b der Wert null zugewiesen wird. In den Zeilen 5 bis 8 können Sie andere Daten eingeben.
#!/usr/bin/env python3
#vp_plot_wurf.py
from vpython import *
#Daten
v0=30 #Anfangsgeschwindigkeit m/s
alpha=45 #Abwurfwinkel °
d=0.22 #Durchmesser fuer Fussball in m
m=0.45 #Masse der Kugel in kg
dt=1e-3 #Zeitschtittweite
xmax = 100 #m
g=9.81 #m/s^2
cw=0.2 #Stroemungswiderstandskoeffizient
rho=1.225 #Luftdichte in kg/m^3
#Berecnungen
A=pi*(d/2)**2 #Querschitt der Kugel
b=1/2*rho*cw*A #Reibungskonstante
#Funktionsdefinition fuer schiefen Wurf
def wurf(v0,alpha,b):
alpha=radians(alpha) #Radiant
tw=2*v0*sin(alpha)/g #Wurfzeit fuer idealen Wurf
vx=v0*cos(alpha)
vy=v0*sin(alpha)
x=y=0
#Lösung der DGL mit dem Euler-Verfahren
for _ in arange(0,tw,dt):
v=sqrt(vx**2 + vy**2)
vx = vx - b*vx*v/m*dt
vy = vy - g*dt - b*vy*v/m*dt
x = x + vx*dt
y = y + vy*dt
if (b==0):
yg1.plot(x,y)#ideal
else:
yg2.plot(x,y)#real
#fuer Beschriftungen
graph(title='Schiefer Wurf',\
xtitle='x in m',\
ytitle='y in m',\
xmin=0,xmax=100,\
ymin=0,ymax=25)
#Objekte fuer Funktionsdarstellung erzeugen
yg1 = gcurve(color=color.blue,width=2,label='ideal')
yg2 = gcurve(color=color.red,width=2,label='real')
#Funktion aufrufen und Kurven zeichnen
wurf(v0,alpha,b)#real
wurf(v0,alpha,0)#ideal
Mit dem Aufruf der selbstdefinierten Python-Funktion wurf(v0,alpha,0) in der letztem Zeile wird der Bewegungsverlauf ohne Luftreibung dargestellt.
Als Einstieg werden die beiden Animationen des idealen und realen schiefen Wurfs vorgestellt und miteinander verglichen. Es soll die Frage geklärt werden welche der beiden Animationen der Realität entspricht. Anschließend werden die Formeln für den idealen Wurf hergeleitet. Das VPython-Programm für die Animation des idealen Wurfs kann jetzt entwickelt werden oder der Quelltext wird vorgegeben und analysiert. In der Testphase werden die Einflüsse der Anfangsgeschwindigkeit und des Abwurfwinkels auf die Wurfweite untersucht.
Schülerexperimente mit realen Tennisbällen und realen Fußbällen sollen auf die Problematik des Luftwiderstandes hinweisen. Die Formel des Luftwiderstandes wird entweder hergeleitet oder vorgeben und eingehend analysiert. Jetzt kann das Differenzialgleichungssystem aufgestellt und analysiert werden. Der Summenalgorithmus des Euler-Verfahrens zeigt anschaulich, dass die Lösung von Differenzialgleichungen etwas mit dem Integrieren zu tun haben muss.
Zum Abschluss können die Funktionsplots erstellt werden. Bei der Erarbeitung der Gesetzmäßigkeiten des schiefen Wurfs handelt es sich nicht um einen linearen Lernprozess, sondern eher um zirkuläre Lernaktivitäten, die bei Bedarf an vorangehende Lernschritte wieder neu anknüpfen. Häufige Wiederholungen und (auch mechanische) Rechenübungen sind unerlässlich um das Gelernte zu festigen. Durch die Programmierung wird der Verstand gezwungen sich intensiver mit einem physikalischen Phänomen auseinanderzusetzen. Diese Aussage provoziert die Frage: Lohnt sich dieser zusätzliche Aufwand überhaupt? Er lohnt sich deshalb, weil er die Selbstwirksam des Lernenden steigert. Am Ende des Lernprozesses steht ein funktionierendes und selbsterstelltes Produkt.
Besuchen Sie die Seite von VPython.
Startseite | NumPy | Matplotlib | SciPy | SymPy