Symbolische Mathematik mit SymPy

Das Modul SymPy verfügt zwar über ähnliche Leistungsmerkmale wie Maple, Mathematica oder Maxima, jedoch erreicht es nicht deren vollen Funktionsumfang. Gegenüber diesen Computeralgebrasystemen (CAS) hat es aber den besonderen Vorteil, dass SymPy-Programme vergleichbar einfacher und flexibler erstellt werden können.

In der Tabelle sind häufig genutzte SymPy-Befehle aufgelistet.

Das nachfolgende Konsolenbeispiel zeigt, dass die in der Tabelle aufgeführten Methoden eigentlich Funktionen sind:

>>> from sympy import *
>>> type(apart)
<class 'function'>
>>> type(cancel)
<class 'function'>
>>> type(Sum)
<class 'sympy.core.assumptions.ManagedProperties'>
>>> type(evalf)
<class 'module'> 

Auf einge SymPy-Funktionen kann man über Objekte zugreifen. In diesem Fall sind sie also Methoden. Damit SymPy-Funktionen nicht mit mathematischen Funktionen verwechselt werden, ist es sinnvoll alle SymPy-Funktionen als Methoden zu bezeichnen.

Das Konsolenbeispiel veranschaulicht die obige Aussage:

>>> type(diff)
<class 'function'>
>>> y = x**2
>>> type(y.diff)
<class 'method'>

Differenzieren und Integrieren

Mit dem Befehl diff(y,x) kann die Ableitung einer Funktion ermittelt werden. Das Integral einer Funktion wird mit dem Befehl integrate(y,x) symbolisch berechnet. Die Befehle können direkt in die Phyton Shell eingegeben werden.

>>> from sympy import *
>>> x=symbols('x')
>>> y=x**3-2*x**2+10
>>> diff(y,x)
3*x**2 - 4*x
>>> diff(y,x,2)
2*(3*x - 2)
>>> integrate(y,x)
x**4/4 - 2*x**3/3 + 10*x

Lösen von Differentialgleichungen

Mit SymPy können nur lineare Differentialgleichung und Differentialgleichungssysteme gelöst werden. Am Beispiel eines Federpendels und eines gekoppelten Federpendels wird gezeigt, wie mit SymPy Differentialgleichungen implementiert werden.

Federpendel

Eine Schraubenfeder ist mit einer Masse verbunden.

Wenn die Masse ausgelenkt und losgelassen wird, schwingt sie hin und her.

Die Schwingungen des Federpendels können durch folgende DGL

\[\ddot{x}+\frac{d}{m} \cdot \dot{x}+\frac{c}{m} \cdot x=0\]

beschrieben werden. Dabei steht d für die Dämpfung.

Gelöst wird die DGL mit der SymPy-Methode dsolve(dgl,ics=aw). Die Abkürzung ics steht für initial/boundary conditions (dt.: Anfangs- bzw. Randbedingungen). Die Abkürzung rhs steht für right hand side also für die rechte Seite einer Gleichung.

#sympy_federpendel.py
from sympy import * 
t = symbols('t')
x = Function('x')
m=1.0   #Masse in kg
d=0.2   #Dämpfung 
c=9.87  #Federkonstante in N/m
x0=5    #Anfangswert x(0)
x_0=0   #x'(0)
dgl=diff(x(t),t,2) + d/m*diff(x(t),t,1) + c/m*x(t)
#Anfangswerte
aw={
    x(0):x0,
    x(t).diff(t,1).subs(t,0):x_0
    }
aL=dsolve(dgl)        #allgemeine Lösung der DGL
sL=dsolve(dgl,ics=aw) #spezielle Lösung der DGL
gL=sL.rhs   #rechte Seite der speziellen Lösung
print("allgemeine Lösung\n",aL)
print("spezielle Lösung\n",sL)
print("Funktionsterm\n x(t) =",gL)
p=plot(gL,(t,0,5),ylabel='x(t)',show=False)
#p.save('federpendel.svg')
p.show()

Ausgabe

Das Beispiel stammt aus meinem Buch "Mathematische Algorithmen mit Python".

Gekoppeltes Federpendel

Zwei Massen sind mit zwei Schraubenfedern verbunden.

Wenn eine oder auch beide Massen ausgelenkt werden, schwingen die Massen in x-Richtung hin und her.

Das Feder-Masse-System wird das durch das folgende DGL-System beschrieben:

\[m_{1}\ddot{x}_{1} + d_{1}\dot{x}_{1}+c_{1}x_{1} - c_{2}\left( x_{2}-x_{1}\right) = 0 \]

\[m_{2}\ddot{x}_{2} + d_{2}\dot{x}_{2} + c_{2}\left( x_{2}-x_{1}\right) = 0 \]

Im Gegensatz zur numerischen Lösung mit der SciPy-Methode solve_ivp(...) muss man dieses DGL-System nicht in ein System 1. Ordnung umwandeln, wenn man die SymPy-Methode dsolve_system(...) nutzt. Diese Methode kann nur lineare Differenzialgleichungen lösen.

#dgl_gekoppeltes_federpendel.py
from sympy import symbols,Eq,Function,plot,N
from sympy.solvers.ode.systems import dsolve_system
t = symbols("t")
x1 = Function("x1")(t)
x2 = Function("x2")(t)
m1,m2=2,2    
c1,c2=10,10    
d1,d2=0.1,0.1 
#DGL-System
dgl1=Eq(m1*x1.diff(t,2) + d1*x1.diff(t,1) + c1*x1 - c2*(x2-x1),0) 
dgl2=Eq(m2*x2.diff(t,2) + d2*x2.diff(t,1) + c2*(x2-x1),0)
aw={
    x1.subs(t,0): 0.1, 
    x2.subs(t,0):-0.1,
    x1.diff(t,1).subs(t,0):0,
    x2.diff(t,1).subs(t,0):0
    }
#Lösung des DGL-Systems
gleichungen = [dgl1,dgl2]
aL=dsolve_system(gleichungen)        #allgemeine Lösung
sL=dsolve_system(gleichungen,ics=aw) #spezielle Lösung
gX1=sL[0][0].rhs 
gX2=sL[0][1].rhs
#Ausgaben
print("allgemeine Lösung\n",aL)
print("spezielle Lösung")
print("x1(t) =",N(gX1,3))
print("x2(t) =",N(gX2,3))
p=plot(gX1,gX2,(t,0,10),show=False,legend=True)
p.xlabel='t'
p.ylabel='Amplitude'
p[0].line_color='blue'
p[0].label='x1'
p[1].line_color='red'
p[1].label='x2'
p.show()

Ausgabe

Laplace-Transformation

Die inverse Laplace-Transformation wird mit der Methode
inverse_laplace_transform(U2_s,s,t)
ermittelt. Die Übertragungsfunktion H(s) ist als algebraischer Ausdruck gegeben.

Das Beispiel zeigt, wie die inverse Laplace-Transformation die Sprungantwort eines R-L-C-Gliedes berechnet.

Die Übertragungsfunktion kann aus der Schaltung entwickelt werden:

\[H\left( s\right) =\frac{U_{2}\left( s\right) }{U_{1}\left( s\right) } =\frac{\frac{1}{Cs} }{R+Ls+\frac{1}{Cs} } =\frac{1}{LCs^{2}+RCs+1} \]

Mit der Sprungfunktion aus dem Bildbereich erhält man die Ausgangsspannung für den Bildbereich:

\[U_{2}\left( s\right) =\frac{U_{1}}{s} \cdot \frac{1}{LCs^{2}+RCs+1} \]

Die Sprungantwort wird in Zeile #2 berechnet.

#berechnet die Sprungantwort für eines R-,L-,C-Gliedes
from sympy import *
s,C,L,R = symbols("s C L R")
t = symbols("t",positive=True)
U1=10
R=2
L=Rational(1,2)
C=Rational(1,4)
U1_s=U1/s
Z_s=R+L*s+1/(C*s)
I_s=U1_s/Z_s
H_s=1/(R + L*s + 1/(C*s))/(C*s)
H_s=expand(H_s) #Übertragungsfunktion
U2_s=U1_s*H_s   #Sprungantwort
uc=inverse_laplace_transform(U2_s,s,t)
ic=inverse_laplace_transform(I_s,s,t)
#Ausgaben
print("Übertragungsfunktion\n",H_s)
print("Spannung am Kondensator\n","uc =",simplify(uc))
print("Kondensatorstrom\n","ic =",ic)
plt=plot(uc,ic,(t, 0, 5),show=False)
plt[0].line_color = 'b'
plt[1].line_color = 'r'
plt.show()       

Ausgabe

Analyse

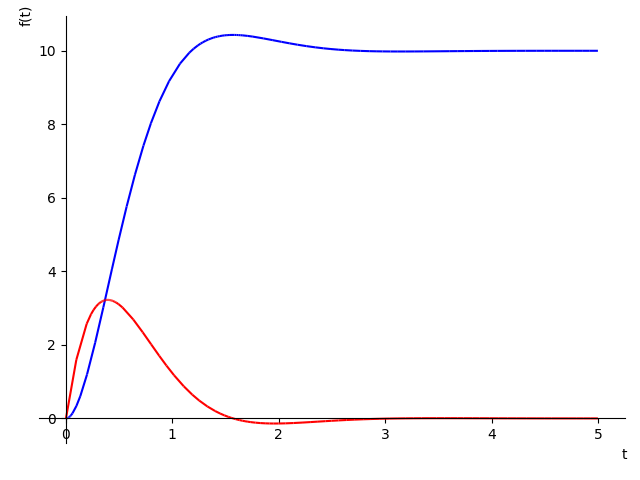
In Zeile #1 steht die Übertragungsfunktion des R-L-C-Gliedes. In den Zeilen #2 und #3 berechnet die inverse Laplace-Transformation die Ausgangsspannung und den Kondensatorstrom des Zweitors (Übertragungssystem).

Besuchen Sie die Seite von SymPy.

Startseite | NumPy | Matplotlib | SciPy | VPython