Animationen

Unter einer Animation versteht man die computergestützte Erzeugung von bewegten Bildern, die den Eindruck einer Bewegung erzeugen. Dies geschieht, indem eine Reihe von Einzelbildern (Frames) schnell hintereinander erzeugt und angezeigt werden. Mit den Python-Modulen Matplotlib und VPython sowie mit Julia können anspruchsvolle Animationen erstellt werden. Durch realitätsnahe Visualisierungen veranschaulichen sie physikalischer Vorgänge. Schnelle, mit dem bloßen Auge nicht mehr sichtbare Vorgänge, wie z.B. Wurfbewegungen, können verlangsamt dargestellt werden.

Animation des schiefen Wurfs

In vielen Sportdisziplinen (Golf, Tennis, Fußball, Handball, Kugelstoßen, Hammerwurf, usw.) kommt der schiefe (oder schräge) Wurf vor. Den Physiker interessiert unter anderem die Form der Wurfbahn, die Wurfzeit, die Wurfweite und die Wurfhöhe. Die Wurfbahn soll mit Python und Julia animiert werden. Die Anfangsgeschwindigkeit v₀ und der Abwurfwinkel α sind die wichtigsten Einflussgrößen auf die Wurfweite. Der Luftwiderstand soll vernachlässigt werden.

Das Bild zeigt eine Wurfbahn. Zu verschiedenen Zeitpunkten sind die Geschwindigkeitskomponenten eingezeichnet.

Im Maximum der Kurve verschwindet die y-Komponente des Geschwindigkeitsvektors.

Der Geschwindigkeitsvektor kann in seine x- und y-Komponente zerlegt werden. Für x-Komponente des Geschwindigkeitsvektors gilt dann:

\[ v_{x}=v_{0}\cos \left( \alpha \right) \qquad (1)\]

Während der gesamten Wurfdauer ist die Geschwindigkeitskomponente in x-Richtung konstant.

Für y-Komponente des Geschwindigkeitsvektors gilt entsprechend:

\[v_{y}=v_{0}\sin \left( \alpha \right) - g\cdot t \qquad (2)\]

Gl. (2) hat eine  bei t₁ = v₀·sinα/g ein Maximum. Bis zu dem Zeitpunkt t < t₁ zeigt y-Komponente des Geschwindigkeitsvektors in Richtung der positiven y-Achse. An der Stelle t = t₁ ist die y-Komponente des Geschwindigkeitsvektors gleich null. Für t > t₁ zeigt y-Komponente des Geschwindigkeitsvektors in Richtung der negativen y-Achse.

Durch Integration von Gl. (1) und Gl. (2) erhält man die Wegkomponenten. Für die x-Komponente des Weges gilt dann:

\[\ x=v_{0}\cos \left( \alpha \right) \cdot t \qquad (3)\]

und für die y-Komponente des Weges gilt:

\[\ y\ =v_{0}\sin \left( \alpha \right) \cdot t\ -\ \frac{1}{2} g\cdot t^{2} \qquad (4)\]

Wenn man Gl. (3) nach t auflöst und in Gl. (4) einsetzt, erhält man die Gleichung einer nach unten geöffneten Parabel:

\[ y=\tan \left( \alpha \right) \cdot x-\ \frac{g}{2v_{0}^{2}\cos^{2} \left( \alpha \right)} x^{2} \qquad (5)\]

Ein geworfener Ball bewegt sich also auf einer parabelförmigen Wurfbahn.

Die Wurfzeit t_w erhält man, indem man Gl. (4) gleich null setzt und die Gleichung nach t auflöst:

\[t_{w}=\frac{2v_{0}\sin \left( \alpha \right)}{g} \qquad (6)\]

Die Wurfweite x_w erhält man, indem man Gl. (6) in Gl. (3) einsetzt:

\[\ x_{w}=\frac{v_{0}^{2}\sin \left( 2\alpha \right)}{g} \qquad (7)\]

Die Wurfhöhe h_w erhält man, indem man die halbe Wurfzeit von Gl. (6) in Gl. (4) einsetzt:

\[\ h_{w}=\frac{v_{0}^{2}\sin^{2} \left( \alpha \right)}{2g} \qquad (8)\]

Lösung mit Matplotlib

Matplotlib stellt die Methode
FuncAnimation(fig,func,frames=n,interval=ival, ...)
für Animationen zur Verfügung. Dieser Methode müssen ein fig-Objekt und eine selbstdefinierte Python-Funktion übergeben werden. Der dritte Parameter legt die Anzahl der Frames (Bilder), die im Zeitintervall ival (vierter Parameter) nacheinander angezeigt werden sollen, fest. Als Standardwert sind 200 ms vorgeben.

Mit dem Matplotlib-Programm ani_wurf.pykönnen Sie einen schiefen Wurf animieren.

#ani_wurf.py
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
#Daten
v0=20      #Anfangsgeschwindigkeit in m/s
winkel=45  #Abwurfwinkel in °
g=9.81     #m/s^2
dt=5e-3    #Zeitschrittweite
alpha=np.radians(winkel)
xmax,ymax=42,12
#Wurfbahn berechnen
def wurfbahn(i):                                                    #1
    t=i*dt
    x=v0*np.cos(alpha)*t
    y=v0*np.sin(alpha)*t-0.5*g*t**2
    ball.set_data([x],[y])                                          #2             
    return ball,
#Grafikbereich
fig,ax=plt.subplots(figsize=(8,4))
ax.axis([0,xmax,0,ymax])
tw=2*v0*np.sin(alpha)/g #Wurfzeit
t=np.arange(0,tw,dt)
ball, = ax.plot([],[],'ro',markersize=10) #Ball
#Animation
ani=FuncAnimation(fig,wurfbahn,frames=t.size,interval=20,blit=True) #3
#Achsenbeschriftungen
ax.set(xlabel="$x$ in m",ylabel="$y$ in m")
plt.show()

Ausgabe

Analyse

In der Selbstdefinierten Python-Funktion wurfbahn(i) (#1) werden die x,y-Koordinaten berechnet und der Matplotlib-Methode set_data([x],[y])

Lösung mit VPython

Mit VPython können Körper wie z.B. Kugeln (sphere), Zylinder (cylinder), Kegel (cone), Quader (box), Pyramiden (pyramid) usw. im 3D-Raum dargestellt und animiert werden. Unter Animationen wird hier die schnelle Abfolge von statischen Bildern verstanden: Die Körper bewegen sich realitätsnah im 3D-Raum auf dem Bildschirm. Solche Darstellungen werden als Szene bezeichnet. Wurf- und Pendelbewegungen lassen sich so anschaulich darstellen. Animationen werden innerhalb einer while-Schleife ausgeführt:

while True:
    rate(n)
    ...

Die rate(n)-Anweisung hält Berechnungen bei Bedarf lange genug an, um sicherzustellen, dass mindestens 1/n Sekunde vergangen ist.

In einem VPython-Programm ist die Funktion rate() ist ein wesentlicher Bestandteil der Animationsschleife. rate(n) erfüllt vier wichtige Aufgaben:

• Erstens bestimmt rate(n) die tatsächliche Ausführungsgeschwindigkeit einer Schleife. Bei rate(1) kann die Schleife maximal einmal pro Echtzeitsekunde ausgeführt werden. Bei rate(500) kann die Schleife bis zu 500 Mal pro Echtzeitsekunde ausgeführt werden. Eine Schleife mit rate(30) sieht auf jedem Computer gleich aus, unabhängig von der CPU-Geschwindigkeit.
• Zweitens sorgt rate(n) für die Ausführung von Animationen. Es gibt VPython Zeit, das Bild neu zu zeichnen, sodass Objekte bewegt, Animationen ausgeführt und Diagramme erstellt werden können. VPython zeichnet jedes Bild nach Möglichkeit 60 Mal pro Sekunde neu. Dies geschieht jedoch nicht ohne eine rate()-Anweisung. Ohne eine rate()-Anweisung aktualisiert die Schleife zwar die Positionen von Objekten, dies ist jedoch nicht sichtbar, da das Bild nicht neu gezeichnet wird.
• Drittens ermöglicht rate(n) die Verarbeitung von Maus- und Tastaturereignissen. Eine Schleife ohne rate()-Anweisung sperrt diese bis zu ihrer Beendigung.
• Viertens macht rate(n) eine Endlosschleife unterbrechbar. Mit einer rate()-Anweisung innerhalb einer Schleife können Sie diese durch Klicken auf „Dieses Programm bearbeiten“ beenden. Ohne rate()-Anweisung bleibt das Programm hängen, und die einzige Möglichkeit besteht darin, den Browser-Tab zu schließen.

Das Bild zeigt den Screenshot des VPytnon-Programms vp_wurf.py.

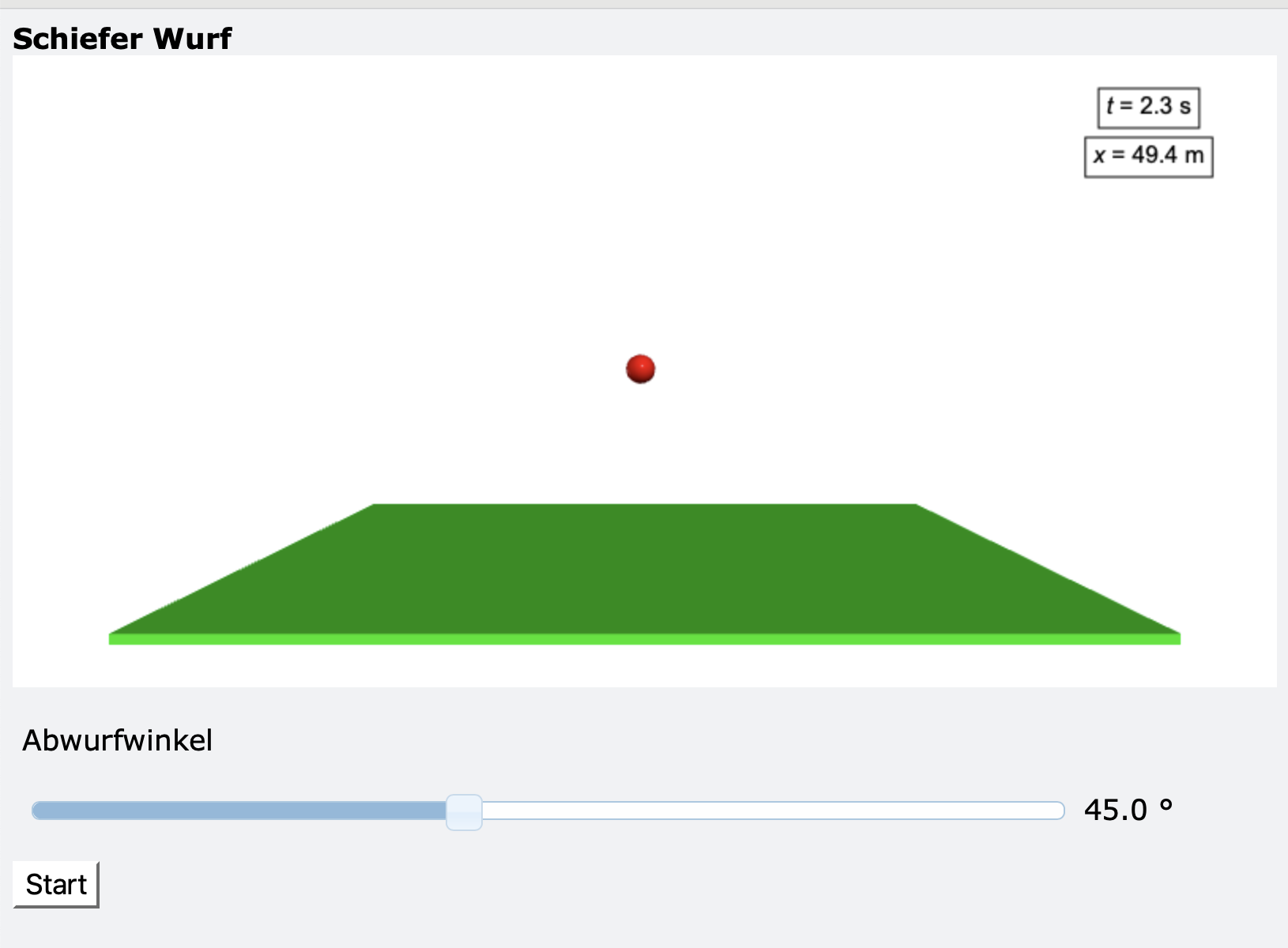
Durch Verschieben des Slider-Knopfes können Sie den Einfluss des Abwurfwinkels auf die Wurfzeit und Wurfweite untersuchen.

#!/usr/bin/env python3
#vp_wurf.py
from vpython import *
#Daten
v0=30      #Anfangsgeschwindigkeit
R = 2      #Z6: Radius des Balls
laenge=100 #Z7: Länge der Bodenplatte
dicke = 1  #Hoehe der Bodenplatte
g=9.81     #Erdbeschleunigung
dt=1e-2    #Zeitschrittweite
...
#Animationsschleife
t=x=y=tw=0
while True:
    rate(30)
    if not run:
        alpha=radians(sldWinkel.value)
    if run:
        x = v0*cos(alpha)*t
        y = y0 + v0*sin(alpha)*t - g*t**2/2
        ball.pos=vec(x - laenge/2,y,0)
        tw=t 
        t+=dt
        if y < y0: #Ball erreicht den Boden
            t=y=0  #Z63
            run = False
            if run == False:
                cmdS.text="Start"
    #Ausgabe für Wurfzeit und Wurfweite
    lblTw.text = 't = %2.1f s' %tw
    lblXw.text = 'x = %2.1f m' %x

In Zeile 6 wird der Radius des Balls mit zwei Längeneinheiten (LE) festgelegt. Dieser Wert ist im Vergleich zur Länge von 100 LE (Zeile 7) nicht maßstabsgetreu. Ein Fußballfeld hat eine Länge von 105 m. Ein normaler Fußball hat einen Durchmesser von 22 cm. Ein Fußballfeld ist also um den Faktor 477 länger als der Durchmesser eines Fußballs. Das Verhältnis von Fußballdurchmesser zu Fußballfeld beträgt also etwa 2 ‰. Bewegen Sie die Szene mit der rechten Maustaste. Sie können so den Wurf aus verschiedenen Perspektiven beobachten. Ermitteln Sie den Abwurfwinkel für die maximal mögliche Wurfweite. Überprüfen Sie, ob die von Programm ermittelte Wurfweite realistisch ist.

Mit dem Programm vp_wurf.py können Sie die Momentangeschwindigkeiten näherungsweise bestimmen, indem Sie die Ausführung an verschiedenen Wurfpositionen anhalten, die zugehörigen Zeiten und Wegabschnitte aufschreiben und aus den Differenzen die Geschwindigkeiten v_i = Δs_i/Δt_i berechnen.

Den vollständigen Quelltext anzeigen.

Lösung mit Julia

In Julia muss zunächst eine Funktion definiert werden, die den Bewegungsablauf beschreibt.

#ani_wurf.jl
using Plots
#Daten
winkel=pi/4 #Abwurfwinkel in rad
v0=20       #Anfangsgeschwindigkeit in m/s
dt=1e-2     #Zeitschrittweite in Sekunden
g=9.81
hw=v0^2*(sin(winkel))^2/(2*g) #Wurfhöhe
xw=v0^2*sin(2*winkel)/g       #Wurfweite
#Wurfbahn
function wurf(i)                                 #1
    t=i*dt
    x=v0*cos(winkel)*t
    y=v0*sin(winkel)*t-1/2*g*t.^2
    scatter([x],[y],xlims=(0,1.1*xw),ylims=(0,1.1*hw),
    markersize=4,color=:red,
    legend=false,xlabel="x in m",ylabel="y in m",ratio=1,grid=false)
end
#Animationsfunktion
ball=@animate for i in 0:1:500                   #2
    wurf(i)
end
gif(ball)                                        #3
gif(ball,"wurf.gif",fps=25)                      #4

Ausgabe

Analyse

Animation eines Fadenpendels

Gezeigt werden soll, wie mit Python (Matplotlib) und VPython die Pendelbewegung eines Fadenpendels im animiert werden kann.

Die Pendelbewegung eines Fadenpendels wird durch zwei Differenzialgleichungen erster Ordnung beschrieben:

\[\frac{d\varphi }{dt} =\omega \]

\[\frac{d\omega }{dt} =-\frac{g}{l} \sin \varphi \]

Dieses DGL-System lässt sich leicht mit einfach zu implementierende und ressourcenschonende Euler-Verfahren numerisch lösen.

Der Quotient aus der Gravitationskonstanten g und der Pendellänge l bestimmt die Anzahl der Schwingungen pro Sekunde (Frequenz f). Für die Frequenz gilt:

\[f=\frac{1}{2\pi} \sqrt{\frac{g}{l}}\]

Lösung mit Matplotlib

Mit dem Programm ani__fadenpendel.py können Sie die Bewegungen eines Fadenpendels animieren. In #1 können Sie den Auslenkwinkel (in °) ändern.

#ani__fadenpendel.py
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
#Daten
winkel = 60                                                  #1                                                  
l = 1.0        #Länge des Pendels
d=0            #Dämpfungskonstante
tmax = 50      #Simulationsdauer
g = 9.81       #m/s^2
w02=g/l        #Quadrat der Kreisfrequenz       
#Lösung der DGL mit dem Euler-Verfahren
dt = 5e-3                      #Zeitschrittweite
t = np.arange(0, tmax, dt)     
n=t.size                       #Anzahl der Frames (Bilder)
phi,w=np.radians(winkel), 0.0  #Anfangswerte
x,y = np.empty(n),np.empty(n)                                #2
x[0]=y[0]=0
for i in range(n):
    phi = phi + w*dt                         #Auslenkung
    w = w - w02*np.sin(phi)*dt - d*w*dt      #Winkelgeschwindigkeit
    x[i],y[i] = l*np.sin(phi),-l*np.cos(phi) #x-y-Koordinaten    
#Animationsfunktion
def pendel(i):                                               #3
    stange.set_data([0,x[i]],[0, y[i]])
    kugel.set_data([x[i]],[y[i]])
    return stange,kugel
#Grafikbereich
fig,ax= plt.subplots(figsize=(6, 6))
ax.axis([-1.1*l,1.1*l,-1.1*l,1.1*l])
ax.set_aspect('equal')
ax.plot(0,0,'ko')                               #Lager für Stange
stange, = ax.plot([],[], 'b-', lw=1)            #Stange
kugel, =  ax.plot([],[], 'ro', markersize='15') #rote Kugel für Pendelmasse
ani=FuncAnimation(fig, pendel,frames=n,interval=20,blit=True) #4
ax.set_axis_off()
plt.show()

Ausgabe

Analyse

In #1 wird der Auslenkwinkel festgelegt. Die NumPy-Arrays sind globale Variablen (#2). In #3 wird die Python-Funktion pendel(i) definiert. Der Bezeichner ist frei wählbar. In #4 wird die Animation ausgeführt.

Lösung mit VPython

Das Bild zeigt den Screenshot einer Momentaufnahme des Programms vp_fadenpendel.py.

In Zeile 5 können Sie die Pendellänge ändern. Sie beeinflusst die Schwingungsdauer.

#!/usr/bin/env python3
#vp_fadenpendel.py
from vpython import *
#Daten
phi=45  #Auslenkung in °
l=8     #Länge des Pendels
b=5     #Breite der Decke
R=0.5   #Radius der Kugel
g=9.81  #Erdbeschleunigung
w02=g/l #Quadrat der Kreisfrequenz
phi=radians(phi) 
w=0.     #Anfangswinkelgeschwindigkeit
dt=1e-2  #Zeitschrittweite
#Grafikbereich
scene.width=600
scene.height=600
scene.center=vector(0,l/3,0)
scene.range=1.5*b
scene.background = color.white
scene.userzoom = False    #kein Zoom
decke=box(size=vec(b,b/20.,b/2.),color=color.gray(0.8))
decke.pos=vec(0,l,0)
stange=cylinder(axis=vec(0,l,0),radius=0.05)
stange.pos=vec(0,l,0)
masse = sphere(radius=R,color=color.red)
masse.pos=vec(0,stange.pos.y,0)
#Animationsschleife
while True:               #Endloßschleife
    rate(100)             #Wiederholungen pro Sekunde
    phi=phi + w*dt        #Lösung der DGL 
    w=w - w02*sin(phi)*dt #mit dem Eulerverfahren
    x= l*sin(phi)         #x-Koordinaten berechnen
    y=-l*cos(phi)         #y-Koordinaten berechnen
    stange.axis=vec(x,y,0)
    masse.pos=stange.pos + vec(x,y,0)

Analyse

Nach dem Start des Programms schwingt das Pendel im virtuellen 3D-Raum des Browserfensters. Bei jedem Durchlauf der while-Schleife bewegt sich das Pendel um den Betrag des Winkels w*dt. Durch die Änderung der Zeitschrittweite dt kann man die Geschwindigkeit der Pendelbewegung beeinflussen. Das DGL-System wird mit dem Summenalgorithmus des Euler-Verfahrens gelöst. Die Dämpfung wurde nicht berücksichtigt.

Besuchen Sie die Seite von Matplotlib.

Besuchen Sie die Seite von VPython.

Besuchen Sie die Seite von Julia.

Startseite | Funktionsplots | Matrizen | Differenzieren | Integrieren | Differenzialgleichungen |